We had so many great cover essays for this year's Advent Calendar that we're extending it this time around to include the Octave of Christmas (Christmas Day through New Year's Day). We'll also continue publishing cover essays into the next year, so if you've got an idea, pitch us (email Will or Ander, or ping us on twitter). Happy Holidays! —Will and Ander
AN INCOMPLETENESS THEOREM
*
Proof:
If I do not accept any axioms as truth, then this proof cannot exist.
If this proof cannot exist, then it cannot serve as a prayer.
If this proof is not a prayer, then I am not praying as I write.
If I am not praying right now, then you must not need my prayers.
Last summer, I moved back to my childhood home in Colorado, and trained myself not to pray for you. I spent my time writing on the futon in my brother’s bedroom, surrounded by his outgrown toys, his old Simpsons poster, and the M.C. Escher art books he used to collect. Instead of praying, I wrote in the past tense about things that had not happened yet. I wrote in the second person because I liked the “you” that kept me company while you could not. My brother kept me company, too. Sometimes, we sat on his futon together and drank beers.
You left because you had to. Actually, I was the one that left. That’s how I ended up back home, alone.
When Daisy Pitkin wrote “An Algorithm” about the time her brother spent deployed in Afghanistan, she included, as axioms, pencil rubbings he did of objects on his military base, such as the sole of his combat boot. “But this, of course is not a boot,” she writes of the rubbing. “It’s an image of a boot, a series of thin marks where a pencil came close to the sole of your boot. I think it’s the closeness of this that makes me feel alone in a way I did not expect.”
Last summer, to combat my loneliness, I revisited one of our shared interests. I read part of a book on Gödel’s incompleteness theorem, the part about the lineage, in formal mathematics, from axiom to theorem to proof: “The axiomatic method consists of accepting without proof certain propositions as axioms or postulates…and then deriving from the axioms all other propositions of the system as theorems” (Nagel and Newman). For example, the equidistance postulate, a necessary foundation of Euclidean geometry, states, but doesn’t prove, that parallel lines are everywhere equidistant. The same could be said about railroad tracks, which we assume will never bend inward or intersect—excluding any trick of perspective.
But the notion that the theorem is the progeny of the axiom can be misleading. It doesn’t capture how we really think when we’re trying to learn about a system. Often, the proofs are what come first, when we initially intuit a logical string of if-thens that lead us to some new realm of factual truth. The theorems come next, once we’ve found a way to name what we’ve discovered. The axioms come last, if ever. After all, we might perpetually question what counts as logical.
I didn’t receive any pencil rubbings from you that summer while you lived in the sober house in Chicago. And I didn’t receive any letters from the place where you went to treatment for several hours each day. But at night when I would listen to your voice over the phone as you described which one of the twelve steps you had focused on that day, all I could think about was the distance between your voice and you, between the image and the object it’s traced upon, between the “foundation” of a system and its “superstructure” (Nagel and Newman), and I felt similarly alone.
In mathematics, it is standard to accept axioms as being true without any proof of their validity. But even then, certain axioms and postulates have been proven false or contradicted after their conception. For this reason, many axioms have yet to be agreed upon. Instead, we pray that they are true. We pray the parallel lines will never intersect, and yet sometimes they do. I prayed for a way to stop praying for you, for a way to be certain you would get better, and yet sometimes I still dipped my forehead into my cupped hands and whispered your name. My axioms sometimes failed me.
I’m trying to learn to be more trusting, but there will always remain some inconsistencies in my faith. It’s one thing to accept an axiom without any proof. It’s another to accept a proof without any axioms.
Incompleteness Theorem: For any formal effectively generated theory T including basic arithmetical truths and also certain truths about formal provability, T includes a statement of its own consistency if and only if T is inconsistent. (Gödel)
Axiom:
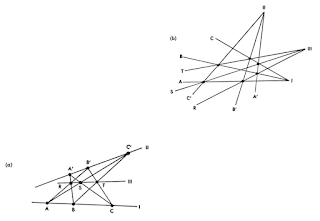
“Fig 2. Two line segments in [one plane] are two segments of great circles in [another plane], and these, if extended, indeed intersect, thus contradicting the parallel postulate.”—Nagel and Newman, Gödel’s Proof, 1958
Axiom:
“Step 2: [We] came to believe that a power greater than ourselves could restore us to sanity.
“To clergymen, doctors, friends, and families, the alcoholic who means well and tries hard is a heartbreaking riddle. To most A.A.’s, he is not. There are too many of us who have been just like him, and have found the riddle’s answer. This answer has to do with the quality of faith…This has been our blind spot.” —Bill W., the co-founder of Alcoholics Anonymous, writing in the past tense about something that you have yet to accomplish, if ever.
Proof:
- If I find my way to the end of this proof, then I will have proven a theorem, even if I don’t know how to name it.
- If I prove this theorem, if I prove all my theorems, then I might, like Pitkin, be able to string my results across an essay.
- Then the proofs themselves will become the story I tell myself.
- If I am able to write this story, then I too, might be able to write you are alive, and then, you will come home whole.
- And if you will come home whole, then you will come home sober, finally.
You said, “The first step was easy. I already knew my life had become unmanageable.” It was the second step that tripped you up, the act of accepting that there exists a higher power that could return you to sanity. You told me that when you confided in a friend at the sober house about your inability to accept the possibility of a higher power, they suggested you simply pray to everything that is Not You. I imagined you kneeling at the foot of your bed, asking for sanity from the liminal space that separated you from the rest of the world. Your imprint.
This method would, given the distance between us, involve praying to me as well.
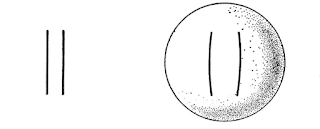
The incompleteness theorem necessitates the existence of a higher power, I’m sorry, a higher order logic. That is, to prove the consistency of one system, one must introduce another system with stronger semantics and more sweeping quantifiers. But the consistency of this new system must then also be proven. These orders of logic build upon themselves infinitely, each layer projecting onto the layer below it. Like the sphere onto the disk onto the line.
Pitkin writes about the residential house in Rheydt, Germany where the artist Gregor Scheinder lived during the 1980s. “He spent his time multiplying the structure of the house within itself: wall in front of wall, ceiling below ceiling, floor on floor, room in room.” She then goes on to contemplate the original structure: “…I wonder if any part of him wishes to burn it down. Maybe not the entire house, but one layer of it—the eighth wall, but not the ninth, not the tenth. Going back in time to take away or implant events that cannot be undone.” If I could undo certain events but not others, I imagine it would be easier for me to trust. But everything in this world has cause and significance.
This is my theory: I am the one who is at risk of Infinite Regress. It’s true that at any moment, you could walk out from the treatment center and down the block to the Binny’s for some Wild Turkey, and this relapse would count as a regression. But I worry more for myself. I worry I’m always going to need proof—proof that you will be safe, proof that you will stay sober, proof of a higher power to restore me to sanity—even when I know that some true facts are necessarily unprovable.
There exists a family video of me traversing the depths of our home before we added the foundation. I remember the hole that was dug into the earth, then filled with layer upon layer of concrete and bright wiring and copper pipes and more concrete. I was crudely digging up clods of dirt with a shovel taller than me. Trying to reach the bottom of something bottomless.
Infinite Regress: One of three parts to a theory that purports the impossibility to prove any truth logically or mathematically. An Infinite Regress arises if the truth of proposition P1 requires the support of proposition P2, the truth of proposition P2 requires the support of proposition P3,…, and the truth of proposition Pn-1 requires the support of proposition Pn and n approaches infinity. (Albert)
Axiom:
[Screenshot of Pete Edward’s 3D Model of M.C. Escher's 1945 “Three Spheres I” woodcut]
“‘Three Spheres’ is a working drawing in which [Escher] meticulously experiments how to convey a sphere on flat paper. Of course, it is still a piece of paper, but all those meticulously drawn lines make us believe that we are in fact looking at three spheres. While the top one is easy to see, the second, middle sphere is a disk which in Escher’s words is:
“‘folded in two halves: a vertical piece and a horizontal piece, on top of which the top sphere rests. But the disk can also be depicted like a round table top, at the bottom of the print, without a fold.’” —Micky Piller, former curator at Escher in Het Paleis, “The Illusion of a Dragon”
Axiom:
“The Hungarian mathematician Johann Bolyai (1802-1860)… spent much of a lifetime in a futile attempt to prove [the equidistance postulate]. [His father], however, knew all too well the difficulties…and wrote this strong warning to his son:
“‘You must not attempt to approach the parallels. I know this way to its very end. I have traversed this bottomless night, which extinguished all light and joy in my life… leave the science of parallels alone.’” —William Dunham, Journey through Genius, 1990
Proof
- If I approach the parallels in this proof, then I will learn it is impossible to prove that parallel lines are everywhere equidistant.
- If I accept this impossibility, then I will have reached the limits of my logic, where I must choose between contradicting myself or accepting a new axiom.
- If I am forced to choose between inconsistency and incompleteness, I will have to accept the latter; that is, I will have to accept that I can’t know everything.
- If I accept that I can’t know everything, I will have to operate on a degree of faith.
Traveling east between Pitkin and her brother involves traversing seven countries, an ocean, and a sea…There are more than twelve thousand miles. The summer I spent alone, the distance between us was considerably smaller. Traveling west towards Colorado from downtown Chicago where I said goodbye to you, I passed through two Midwest states on i-80 and over one major river (Mississippi), but through no oceans, seas, or mountain ranges. I used to make this trip by train.
What else can be proven about this distance? What else can be proven about the distance between parallel lines, except that they eventually meet at the horizon?
When you came to stay with me in my childhood home at the end of the summer, I was careful not to ask you too much. Excusing myself of the fear of having to know by telling myself that you wouldn’t want to say. I didn’t want to know if or when you had faltered in your belief that you would get better. And I didn’t want to reveal how little I wanted to know. We laid in bed together and stared at each other in silence. I made invisible maps of the distance between you and me, between you and Not You.
I had been warned that there were risks entailed in remaining in a romantic relationship with someone who had recently become sober. There was a chance, I was told, that the person in recovery (you) would outgrow the people of their past.
Which would, given the time that’s elapsed between us, involve outgrowing me as well.
But there was also a chance, I hoped, of us recognizing our mirror images in each other, of growing even closer than we used to be. We were both at turning points, after all, both learning to fight off the temptation to regress. The law of excluded middle ensures that one and only one of these two possibilities will occur, lest we reach a contradiction.
Law of Excluded Middle: Of two contradictory propositions, one must be true, the other false: P ∨ ¬ P. (Aristotle)
Axiom:
Fig 3. The two figures have the same abstract structure though in appearance they are markedly different. (a) is so related to (b) that points of the former correspond to lines of the latter, while lines of the former correspond to points of the latter. In effect (b) is a map…(or is the “mirror image” of)…(a).—Nagel and Newman
Axiom:
“What makes the images impressive is the use of movement and perspective, the possibility of sky charts. The point where two railroad tracks come together is the point where they vanish, one new thought that leaves our sight.” —T. Fleischmann, Syzygy, Beauty: An Essay, 2012
Proof:
- If I am enamored by the tools of mathematical proof, then I am beholden to the extremes of logical quantifiers.
- If I am bound to these quantifiers, then I am inescapably aware of each “for every” and “there exists” statement that could undo the foundations of our mutual trust.
- (As in, for every year that we remain together after this summer, there exist 356 days on which you might relapse, on which I’ll stop trusting you, on which you’ll stop trusting me to trust you.)
- And if I am aware that our foundations are in a perpetual state of potentially going to ruins, then I could imagine myself refusing to build any lasting theorems upon them.
- If there are no more theorems, then there are no more proofs, and no prayers.
or (proof as prayer)
- If I am enamored by the tools of mathematical proof, then I am enamored enough to believe that these tools are capable of withstanding my bastardization of them.
- If I can trust myself to bastardize the proof, then I am willing to trust my bastardization of the axiom, too.
- (As in, I can call the symbols meaningless and the truth will persist, I can destroy the image but not the object, I can distrust the blueprint but the foundation will remain intact.)
- And if I can accept my incomplete trust in the axioms, then I can accept that each proof is proof as prayer.
“An Algorithm” ends with two divergent proofs. Either Pitkin can find no way back to her brother, who is enamored by the tools of war, or else his body is still somehow separate…from the war itself, thus furnishing a promise of his eventual return. The law of excluded middle ensures that one and only one of these two possibilities will occur, but it offers no prediction one way or the other. It is up to whoever creates the system to assert these truths that are not provable.
I never fully understood Gödel’s incompleteness theorem, nor is it something, I am realizing, I ever really want to fully understand. The original proof is infamously challenging to decipher, riddled with arcane logical symbols that render it incoherent to amateurs. If I plan to keep my understanding this limited, I can continue to extravagantly misuse the incompleteness theorem whenever I reach an impasse in my faith.
But I know this much: that after he proved the incompleteness theorem in 1931, Kurt Gödel became intoxicated with, or tortured by, the idea that there existed truths beyond the scope of his life. He quaked at the possibility that the intricate network of human minds and relationships were extinguished after death. “That would be approximately as if someone laid the foundation for a house with much effort and expenditure of money, then let everything go to ruin again,” he wrote in a letter to his mother in 1961.
After that summer, we moved back in together. Our foundations haven’t gone to ruins, but I do write about them sometimes, and therein find that I do not truly know what counts as logical. I’ve started to think that maybe every essay, at least every essay of mine, is an incomplete theorem, every story dependent on a string of proofs—the proof by the second person, the proof of the past tense—that are built upon loose earth.
Predicate Calculus: An axiomatic form of predicate logic in which formulas contain variables which can be quantified. Two common quantifiers are the existential ∃ (“there exists”) and universal ∀ (“for all”) quantifiers. (Boole)
Axiom:
“[Gödel] also makes the interesting observation that “it was to be expected” that his incompleteness proof “would be made useful for religion sooner or later, for that is doubtlessly supportable in a certain sense”—suggesting that Gödel himself was more open to embracing philosophical ramifications of his theorem than have been his fellow logicians and philosophers, who are almost uniformly critical of such endeavors (though admittedly often with good reason, given the extravagant misuse of Gödel’s proof in popular culture in recent years.)
“In one sense, to be sure, his religious and philosophical views are marked by [Gödel’s] paranoid, or at least naïve, reasoning…in which he applies rigorously logical inference to a dubious premise, namely that everything that happens in the world has cause and significance.” —Stephen Budiansky, Ever Your Kurt: The Intimate Family Letters of Kurt Gödel, Translated by Marilya Veteto Reese, 2021
Axiom:
[blueprint of my childhood home]
It is not a guarantee that there exists a higher power who will proofread all my unprovable proofs. But if I mean well and try hard, does it matter that I am occasionally inconsistent? This is, at times, a heartbreaking riddle.
*
Martha Strawbridge is a writer living in Iowa City, where she is a rhetoric instructor and MFA candidate in the Nonfiction Writing Program at the University of Iowa. [twitter]




No comments:
Post a Comment